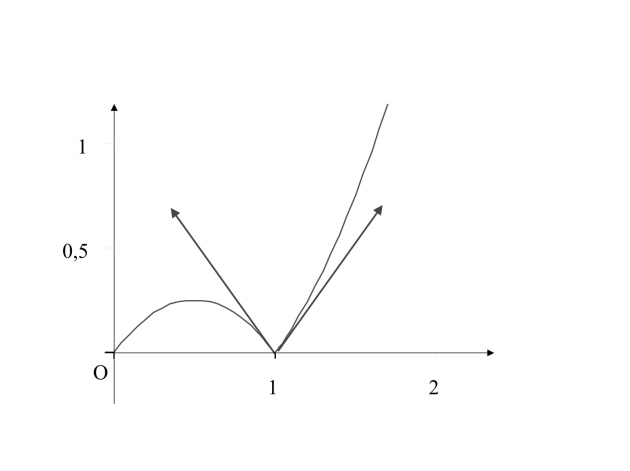
Nombre dérivé à gauche, à droite [ANALYSE

Nombre dérivé à gauche, à droite

La fonction $f : x \to | x (x - 1) |$ est dérivable sur $[0; 1 [$ et sur $] 1; + \infty [$ . Mais au point $x = 1$ , il n'est pas possible de conclure.

On calcule

$\lim_{h \to 0^{+}} \frac{f (1 + h) - f (1)}{h} = \lim_{h \to 0^{+}} \frac{(1 + h) h}{h} = \lim_{h \to 0^{+}} (1 + h) = 1$

$\lim_{h \to 0^{-}} \frac{f (1 + h) - f (1)}{h} = \lim_{h \to 0^{-}} \frac{- (1 + h) h}{h} = \lim_{h \to 0^{+}} (- (1 + h)) = - 1$

La fonction $f$ n'est pas dérivable au point 1, car les limites à gauche et à droite du taux d'accroissement en ce point sont différentes, il n'existe donc pas de nombre dérivé au point 1. La courbe admet au point 1 deux demi-tangentes de coefficients directeurs 1 et -1.

Définition :

Une fonction $f$ définie sur un intervalle $I$ contenant le réel $a$ est dérivable à droite [respectivement à gauche] en $a$ si et seulement si $\lim_{h \to 0^{+}} \frac{f (a + h) - f (a)}{h}$ [respectivement $\lim_{h \to 0^{-}} \frac{f (a + h) - f (a)}{h}$ ] existe et est finie.

Cette limite est alors notée $f_{d}^{'} (a)$ [respectivement $f_{g}^{'} (a)$ ]

$f_{d}^{'} (a)$ et $f_{g}^{'} (a)$ sont les coefficients directeurs des demi-tangentes au point $a$ .

Fondamental : Théorème

Soit $f$ une fonction définie sur un intervalle $I$ contenant le réel $a$ , $f$ est dérivable en $a$ si et seulement si $f$ est dérivable à gauche et à droite en a et $f_{d}^{'} (a) = f_{g}^{'} (a)$ .

De plus, sous ces hypothèses, on a : $f_{d}^{'} (a) = f_{g}^{'} (a) = f^{'} (a)$ .

Définition :

Si $f$ est une fonction dérivable en tout point d'un intervalle $I =] a; b [$ , dérivable à gauche en $b$ et à droite en $a$ , on dit que $f$ est dérivable sur $J = [a; b]$ .