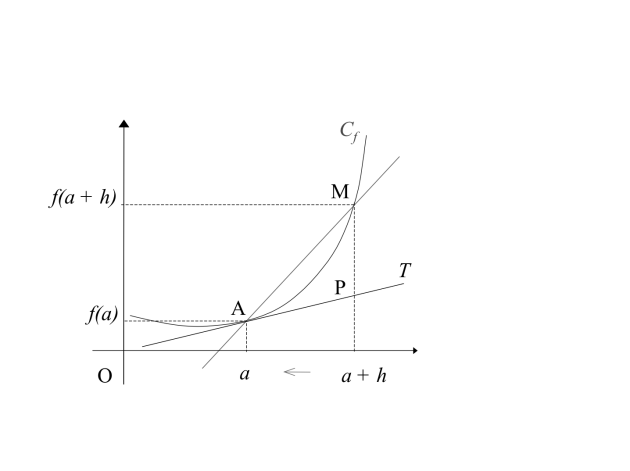
Interprétation géométrique
Soient et deux points de la courbe représentative de . Le coefficient directeur de la droite est égal à :
Lorsque " tend" vers , le point tend vers le point et la droite devient donc tangente à la courbe, et son coefficient directeur devient :
On obtient donc une équation de la tangente à la courbe au point d'abscisse : cette droite passe par le point et admet comme coefficient directeur.
On obtient :