Limite infinie en a. Asymptote verticale. [ANALYSE

Limite infinie en a. Asymptote verticale.

Définition :

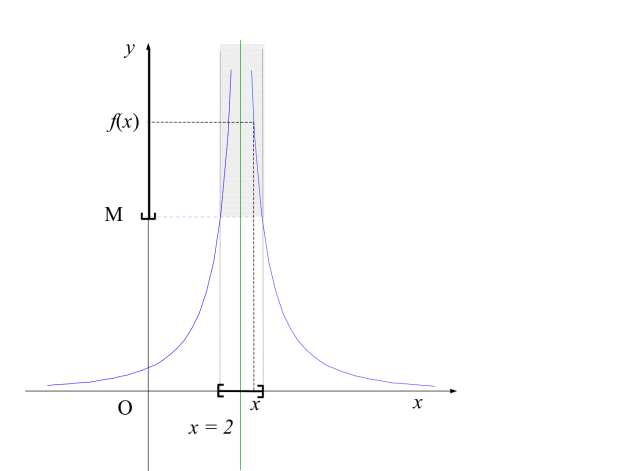
$f$ est une fonction définie sur $I$ sauf peut-être au point $a$ , $M$ est un réel positif, dire que $f (x)$ tend vers $+ \infty$ lorsque $x$ tend vers $a$ signifie que tout intervalle de la forme $[M; + \infty [$ contient toutes les valeurs de $f (x)$ pour $x$ assez voisin de $a$ . On écrit : $\lim_{x \to a} f (x) = + \infty$ ou $\begin{matrix} f (x) \to + \infty \\ x \to a \end{matrix}$

Autrement dit :

$\lim_{x \to a} f (x) = + \infty \Leftrightarrow \forall M > 0, \exists η > 0 / \forall x \in I, | x - a | \leq η \Rightarrow f (x) \geq M$

On dit que $f (x)$ tend vers $- \infty$ lorsque $x$ tend vers $a$ si et seulement si $- f$ admet $+ \infty$ pour limite en $a$ .

Si $\lim_{x \to a} f (x) = + \infty$ ou si $\lim_{x \to a} f (x) = - \infty$ la droite d'équation $x = a$ est asymptote (verticale) à la courbe.

Exemple :

$f$ est définie sur $ℝ - {2}$ par : $f (x) = \frac{2}{{(x - 2)}^{2}}$ .

Dés que $| x - 2 | \leq 0,01$ , on a~: $f (x) \geq 2 \times 10^{4}$

On comprend que tout intervalle de la forme $[M; + \infty [$ contient toutes les valeurs de $f (x)$ pour $x$ assez voisin de 2

On a : $\lim_{x \to 2} f (x) = + \infty$ .

La droite d'équation $x = 2$ est asymptote à la courbe.