La fonction composée x -> exp(u(x))

D'après le théorème sur la fonction dérivée d'une fonction composée, on peut écrire :

FondamentalThéorème

Soit u u une fonction dérivable sur un intervalle I I .

La fonction f : x → e u ( x ) f nitalic : x toward e^{u(x)} est dérivable sur I I et f ' ( x ) = u ' ( x ) e u ( x ) f'(x)=u'(x) e^{u(x)}

En remarquant que, pour tout x x réel, e u ( x ) > 0 e^{u(x)} > 0 , on peut affirmer que la fonction e u e^u a le même sens de variation que la fonction u u .

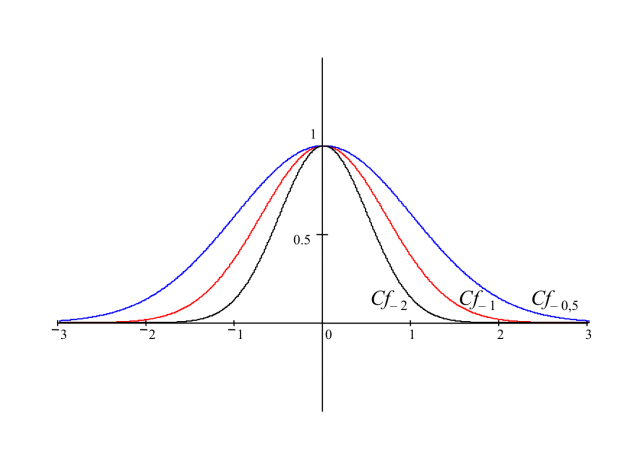
Exemple

Soit f : x → e 2 − x 2 f nitalic : x toward e^{2-x^2}

On a : f ' ( x ) = − 2 x e 2 − x 2 f'(x)=-2 x e^{2 - x^2} , f f est croissante sur ℝ − setR_{{}-{}} et décroissante sur ℝ + setR_{{}+{}} et admet un maximum au point 0, tout comme la parabole d'équation y = 2 − x 2 y = 2-x^2

ExempleFonctions à connaître

Représentations graphiques des fonctions :

f − 1 : x → e − x 2 ; f − 0,5 : x → e − 1 2 x 2 ; f − 2 : x → e − 2 x 2 f_{-1} nitalic : x toward e^{-x^2} " ; " f_{-0,5} nitalic : x toward e^{- {{1} over {2}}x^2} " ; " f_{-2} nitalic : x toward e^{- 2x^2}