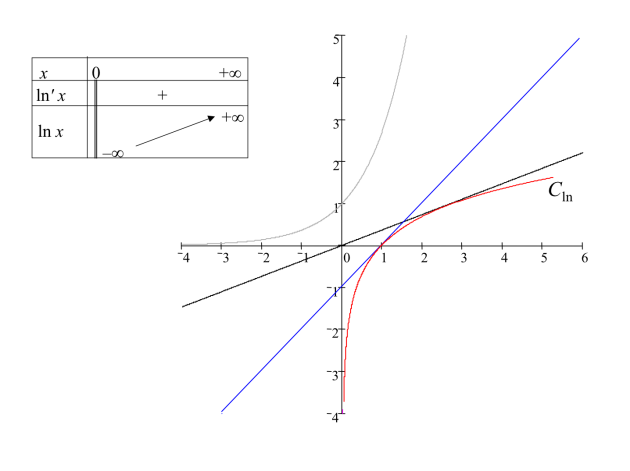
Limites, représentation graphique

FondamentalThéorème

On a :

lim x → + ∞ ln ( x ) = + ∞ ; lim x → 0 ( x > 0 ) ln ( x ) = − ∞ ; lim x → 0 ( x > 0 ) ln ( x ) = 0 ; lim x → + ∞ ln ( x ) x = 0 lim from {x toward +infinity} ln(x)= +infinity ";" lim from {x toward 0 (x>0)} ln(x)= -infinity ";" lim from {x toward 0 (x>0)} ln(x)= 0 ";" lim from {x toward +infinity} {{ln(x)} over {x}}= 0

On en déduit que la représentation graphique de la fonction ln admet une asymptote d'équation x = 0 x = 0 (axe des ordonnées), et une branche parabolique horizontale (d'axe Ox Ox ) lorsque x x tend vers + ∞ "+"infinity .

La tangente à la courbe au point d'abscisse 1 a pour équation : y = x − 1 y = x-1

La tangente à la courbe au point d'abscisse e e passe par l'origine du repère, elle a pour équation : y = x e y = x over e

La représentation graphique de la fonction ln est symétrique de celle de la fonction exponentielle par rapport à la droite d'équation : y = x y = x