Théorème de la moyenne, valeur moyenne d'une fonction sur un segment

Fondamental(Théorème de la moyenne)

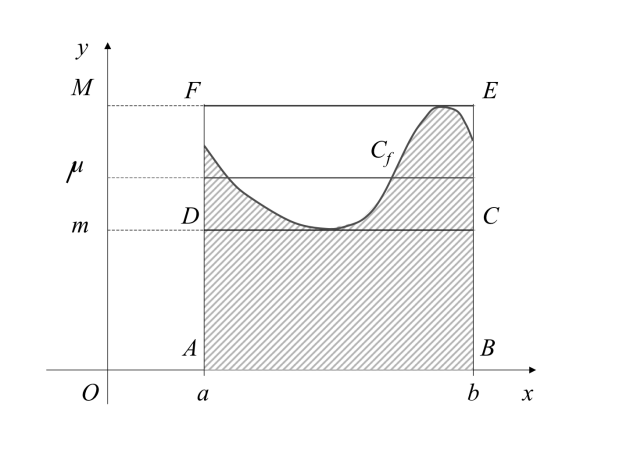
Soient f f une fonction continue sur un intervalle [ a ; b ] left [ a nitalic ; b right ] (avec a ≠ b a<>b ), m m et M M les bornes inférieures et supérieures de f f sur [ a ; b ] left [ a nitalic ; b right ] . Alors il existe μ %mu compris entre m m et M M , tel que ∫ a b f ( x ) dx = μ ( a − b ) int from a to b f(x) dx = %mu (a-b)

On a m ≤ f ( x ) ≤ M m <= f(x) <= M , on en déduit :

∫ a b m dx ≤ ∫ a b f ( x ) dx ≤ ∫ a b M dx int from a to b m dx <= int from a to b f(x) dx <= int from a to b M dx

Et donc :

m ( b − a ) ≤ ∫ a b f ( x ) dx ≤ M ( b − a ) m(b-a) <= int from a to b f(x) dx <= M(b-a)

Enfin

m ≤ 1 b − a ∫ a b f ( x ) dx ( = μ ) ≤ M m <= 1 over {b-a} int from a to b f(x) dx ({}=%mu)<= M

Définition

f f est une fonction intégrable sur un intervalle [ a ; b ] left [ a nitalic ; b right ] , avec a ≠ b a<>b . La valeur moyenne de f f sur [ a ; b ] left [ a nitalic ; b right ] est le réel

μ = 1 b − a ∫ a b f ( x ) dx %mu = 1 over {b-a} int from a to b f(x) dx

Si, de plus, f f est continue sur [ a ; b ] left [ a nitalic ; b right ] , il existe une valeur c c de x x comprise entre a a et b b et telle que μ = f ( c ) %mu = f(c)

Interprétation géométrique

Pour une fonction f f positive sur [ a ; b ] left [ a nitalic ; b right ]

On suppose que m ≤ f ( x ) ≤ M m <= f(x) <= M . L'aire du domaine associée à f f sur [ a ; b ] left [ a nitalic ; b right ] est comprise entre les aires des deux rectangles ABCD ABCD et ABEF ABEF . ( m ( b − a ) m(b-a) est l'aire du rectangle ABCD ABCD et M ( b − a ) M(b-a) celle du rectangle ABEF ABEF )

Cette aire est égale à l'aire du rectangle d'aire μ ( b − a ) %mu(b-a) , μ %mu étant la valeur moyenne de f f sur [ a ; b ] left [ a nitalic ; b right ] :