Intégrale d'une fonction bornée [ANALYSE

Intégrale d'une fonction bornée

Définition

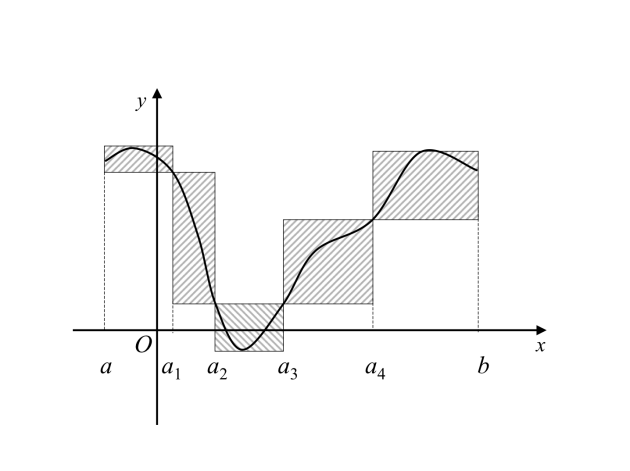
Soit $f$ une fonction réelle de la variable bornée sur $[a; b]$ . Il existe des fonctions en escalier majorant $f$ sur $[a; b]$ , par exemple $e : x \to M$ , $M$ désignant un majorant de $f$ . De même, il existe des fonctions en escalier minorant $f$ sur $[a; b]$ .

Définition : (Fonction bornée intégrable)

Soit $f$ une fonction bornée sur $[a; b]$ , on dit que $f$ est intégrable au sens de Riemann si et seulement si il existe deux fonctions en escalier $u$ et $v$ telles que pour tout $x \in [a; b]$ on ait $u (x) \leq f (x) \leq v (x)$ et dont les intégrales sont arbitrairement voisines.

Autrement dit :

$\forall ε > 0, \exists u \in ε (a; b), \exists v \in ε (a; b) / u \leq f \leq v et \int_{a}^{b} v (x) dx - \int_{a}^{b} u (x) dx < ε$

L'ensemble des réels de la forme $\int_{a}^{b} u (x) dx$ où $u \in ε (a; b)$ et $u \leq f$ sur $[a; b]$ admet une borne supérieure. De même l'ensemble des réels de la forme $\int_{a}^{b} v (x) dx$ où $v \in ε (a; b)$ et $v \geq f$ sur $[a; b]$ admet une borne inférieure.

Si $f$ est intégrable au sens de Riemann, ces deux bornes sont égales à un réel qui s'appelle intégrale de $f$ sur $[a; b]$ que l'on note $\int_{a}^{b} f (x) dx$

Remarque :

Si $f$ est une fonction en escalier on retrouve, bien sûr, la définition 2.1.2

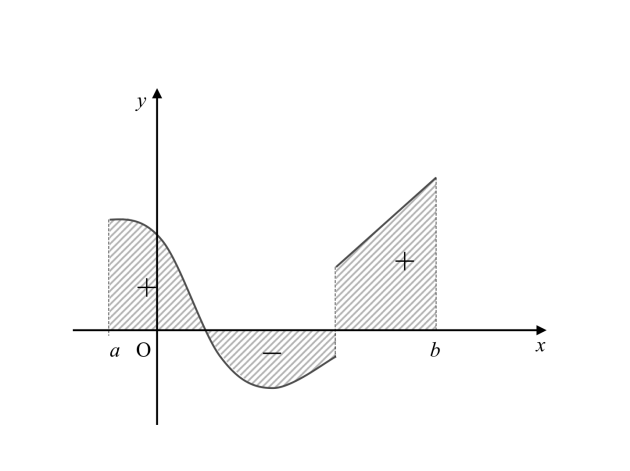
Interprétation graphique

L'aire comprise entre les représentations de $u$ et $v$ est aussi proche de $0$ qu'on le veut :

Continuité et intégrabilité

Fondamental : Théorème

Toute fonction $f$ continue sur $[a; b]$ est intégrable au sens de Riemann sur $[a; b]$

Propriétés fondamentales

$f$ et $g$ sont deux fonctions intégrables sur $[a; b]$ , on a :

$\begin{matrix} \int_{a}^{b} [f (x) + g (x)] dx = \int_{a}^{b} f (x) dx + \int_{a}^{b} g (x) dx \\ \int_{a}^{b} k f (x) dx = k \int_{a}^{b} f (x) dx (k \in ℝ) \end{matrix}$
Si $f$ est positive sur $[a; b]$ , alors $\int_{a}^{b} f (x) dx \geq 0$
Si $f \leq g$ sur $[a; b]$ , alors $\int_{a}^{b} f (x) dx \leq \int_{a}^{b} g (x) dx$
Relation de Chasles
Si $c \in] a; b [$ alors $f$ est intégrable sur $[a; c]$ et $[c; b]$ et :
$\int_{a}^{c} f (x) dx + \int_{c}^{b} f (x) dx = \int_{a}^{b} f (x) dx$
Par convention, on pose :
$\int_{a}^{a} f (x) dx = 0 et \int_{a}^{b} f (x) dx = - \int_{b}^{a} f (x) dx$
La relation de Chasles est alors valable pour $c \in [a; b]$
De plus, on démontre que, $a$ , $b$ , $c$ étant trois réels tels que $a < b < c$ , si $f$ est une fonction intégrable au sens de Riemann sur $[a; c]$ et sur $[c; b]$ alors $f$ est intégrable sur $[a; b]$ et la relation de Chasles est vérifiée.
On tire de cette propriété le théorème suivant qui complète le théorème sur la continuité et l'intégrabilité. Il est très important car il ouvre un champ considérable de fonctions intégrables.

Continuité par morceaux et intégrabilité

Fondamental :

Toute fonction $f$ continue par morceaux sur $[a; b]$ est intégrable sur $[a; b]$

Remarque : Interprétation géométrique de l'intégrale

Il vient immédiatement de la définition que l'intégrale d'une fonction continue par morceaux sur l'intervalle $[a; b]$ est représentée par l'aire algébrique délimitée par la courbe et l'axe des abscisses :

Inégalités et intégration

Fondamental :

Si une fonction $f$ est intégrable sur $[a; b]$ alors $| f |$ est intégrable sur $[a; b]$ et :

$| \int_{a}^{b} f (x) dx | \leq \int_{a}^{b} | f (x) | dx$

Attention :

Ce théorème doit être utilisé dans le bon sens : prenons, par exemple, la fonction $g$ définie par :

$\begin{matrix} g : [0; 1] \to ℝ \\ x \to 1 si x \in ℚ \\ x \to - 1 si x \notin ℚ \end{matrix}$

$| g |$ est intégrable sur $[0; 1]$ mais $g$ ne l'est pas

Fondamental : Inégalité de Schwartz

Soient $f$ et $g$ deux fonctions intégrables sur $[a; b]$ alors $fg$ est intégrable sur $[a; b]$ et :

Nous admettons que $fg$ est intégrable. Soit $k \in ℝ$ on a :

${((f + kg) (x))}^{2} = f^{2} (x) + 2 k f (x) g (x) + k^{2} g^{2} (x)$

Donc :

$\int_{a}^{b} {((f + kg) (x))}^{2} dx = \int_{a}^{b} {(f (x))}^{2} dx + 2 k \int_{a}^{b} f (x) g (x) dx + k^{2} \int_{a}^{b} {(g (x))}^{2} dx$

Or, si $\int_{a}^{b} g^{2} (x) dx \neq 0$ , $\forall k \in ℝ, \int_{a}^{b} {((f + kg) (x))}^{2} dx \geq 0$ , donc le trinôme en $k$ qui constitue le deuxième membre de l'égalité précédente doit être positif quelque soit $k$ , son discriminant doit donc être négatif ou nul, ce qui équivaut à :

${(\int_{a}^{b} f (x) g (x) dx)}^{2} - \int_{a}^{b} {(f (x))}^{2} dx \int_{a}^{b} {(g (x))}^{2} dx \leq 0$

Si $\int_{a}^{b} g^{2} (x) dx = 0$ alors $g = 0$ et l'inégalité est vérifiée.

D'où le résultat.