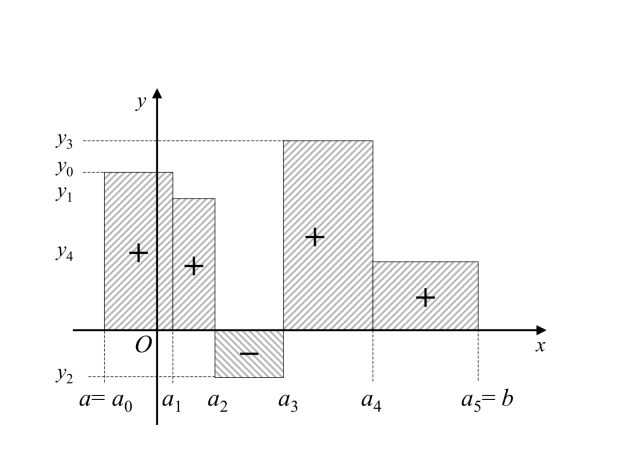
Intégrale d'une fonction en escalier sur un segment [ANALYSE

Intégrale d'une fonction en escalier sur un segment

Définition : (Subdivision d'un intervalle)

On appelle subdivision d'un intervalle $[a; b]$ toute famille finie $s = {(a_{i})}_{0 \leq i \leq n}$ , telle que :

$a = a_{0} \leq a_{1} \dots \leq a_{n} = b avec n \in ℕ, n \geq 1$

Définition : (Fonction en escalier)

Soit $f$ une fonction réelle de l'intervalle $I = [a; b]$ dans $ℝ$ . $f$ est une fonction en escalier si et seulement si il existe une subdivision $s = {(a_{i})}_{0 \leq i \leq n}$ de $[a; b]$ , dite subdivision adaptée à $f$ , telle que $f$ soit constante sur chacun des intervalles $] a_{k}; a_{k + 1} [$ (pour tout $x$ de $] a_{k}; a_{k + 1} [$ , on a $f (x) = y_{k}$ , où $y_{k}$ est une constante réelle)

Remarque :

Les valeurs de $f$ aux points $a_{0}, \dots, a_{i}, \dots, a_{n}$ sont quelconques.

Remarque :

On note $ε (a; b)$ l'ensemble des fonctions en escalier sur $[a; b]$

Définition : (Intégrale d'une fonction en escalier)

Soit $f$ une fonction en escalier sur $I = [a; b]$ on appelle intégrale de $f$ sur $[a; b]$ le réel :

$\int_{a}^{b} f (x) dx = \sum_{k = 0}^{n - 1} (a_{k + 1} - a_{k}) y_{k}$

où $s = {(a_{i})}_{0 \leq i \leq n}$ est une subdivision adaptée à $f$

Remarque :

Le réel $\sum_{k = 0}^{n - 1} (a_{k + 1} - a_{k}) y_{k}$ ne dépend pas de la subdivision adaptée à $f$
L'intégrale de $f$ sur $[a; b]$ est l'aire algébrique des rectangles hachurés de la figure qui suit : on affecte l'aire des rectangles situés au dessus de l'axe $(Ox)$ d'un signe positif et l'aire de ceux situés en dessous de l'axe d'un signe négatif.