ANALYSE - Concours B des ENSA

On appelle fonction logarithme décimal, notée log, la fonction définie sur $\left]0\mathrm{;}+\mathrm{\infty }\right[$ par :

$\log x=\frac{\ln x}{\ln 10}$

Conséquences immédiates :

• La constante $\frac{1}{\ln 10}$ étant positive, on en déduit que la fonction log a le même sens de variation que la fonction ln. Elle est définie et dérivable sur $\left]0\mathrm{;}+\mathrm{\infty }\right[$ et elle est strictement croissante sur cet intervalle.

• La fonction log possède toutes les propriétés algébriques de la fonction ln.

  En particulier : $\log 1=0$, $\log 10=1$, $\log {10}^p=p$ ($p$ entier)

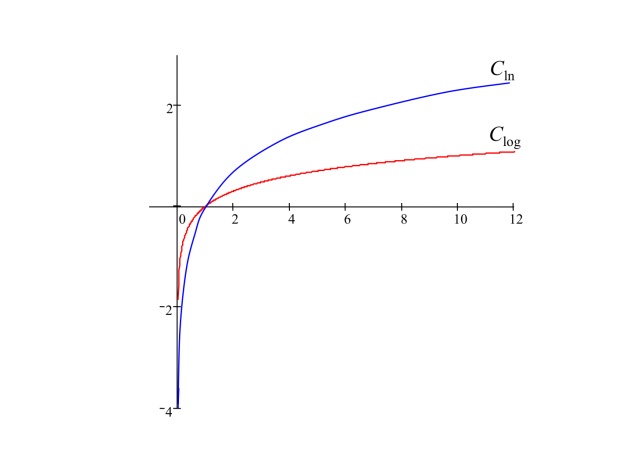
On a représenté sur le même graphique la fonction ln et la fonction log.