Mes pages professionnelles

[14] Thual O., Lacaze L., Mouzouri M., Boutkhamouine B. (2015), Critical slope for laminar transcritical shallow-water flows, J. Fluid Mech, 783, R1, 11pp.

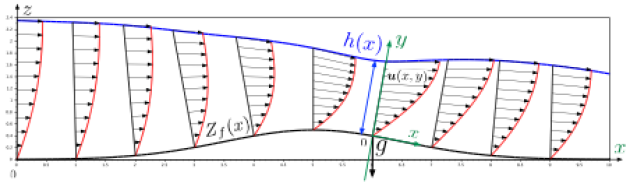
Nous avons développé un nouveau modèle qui permet d'enrichir la description classique des écoulements à surface libre à l'aide des équations de Saint-Venant. Notre modèle permet de calculer simplement les profils de vitesse en fonction de la pente de la surface libre et en tenant compte de la rhéologie du fluide. Il repose sur une hypothèse d'autosimilarité des solutions dont la validité est étudiée dans cet article pour le cas de la transition critique d'un écoulement laminaire newtonien. L'extension de ce modèle à d'autres rhéologies ou régimes est un axe très prometteur.

[21] Thual, O. (2013) Modelling rollers for shallow water flows, J. Fluid Mech., (728) 1-4.

Expertiser des articles scientifiques et être rapporteur de jury de thèses fait partie du métier de l'enseignement chercheur. Cet article, paru dans le section « Focus on fluids » de « Journal of Fluid Mechanics » est le fruit telle activité qui m'a conduit à étudier de très près des recherches innovantes d'une équipe de l'IUSTI sur la modélisation des ressauts hydrauliques et des roll waves. Dans cet article, je mets en relief les verrous scientifiques que ce travail a permis de lever ainsi que les nombreuses perspectives qu'il motive.

[31] Thual, O., Lacaze, L. (2010), 'Fluid boundary of a viscoplastic Bingham flow for finite solid deformations', Journal of Non-Newtonian Fluid Mechanics 165(3-4), 84-87.

En considérant la loi comportement des fluides de Bingham et les critères de rupture des solides élastiques, nous avons montré que la singularité mathématique invoquée dans la plupart des simulations numériques de fluides à seuil devaient être revue en tenant compte d'une approche plus physique. Ce travail est significatif dans la mesure où il est le point de départ d'une nouvelle activité dans l'équipe sur les fluides non-newtoniens.

[32] Thual, O.; Plumerault, L. R.; Astruc, D. (2010), 'Linear stability of the 1D Saint-Venant equations and drag parameterizations', Journal of Hydraulic Research 48(3), 348-353.

Le résultat principal de ce travail a été de montrer rigoureusement que l'instabilité « roll waves » d'un écoulement à surface libre forcé par la gravité était de nature convective pour tout type de paramétrisation du frottement. L'adimensionnalisation de ce problème permet de mettre en évidence que les grandes échelles correspondent à la limite des frottements forts, ce qui justifie l'approximation des ondes cinématiques où il ne subsiste plus qu'une seule branche de modes. Ce travail théorique a été mené conjointement avec les expériences en canal hydraulique sur fond périodique ([30]).

[56] Thual, O., Fauve, S. (1988), ‘Localized Structures Generated by Subcritical Instabilities', Journal De Physique 49(11), 1829-1833.

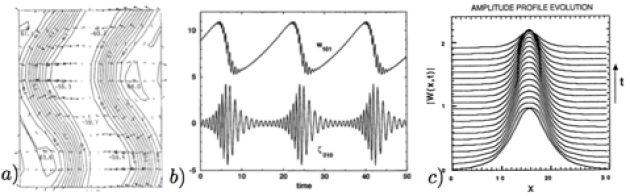
Cité 283 fois, cet article propose une explication générique de l'existence de structures localisées dans les systèmes physiques dont la déstabilisation est réalisée au moyen d'une bifurcation sous-critique. C'est le cas, par exemple, des écoulements parallèles pour lesquels on observe des bouffées de turbulence confinées en espace. Notre modèle repose sur l'équation de Ginzburg-Landau que l'on peut voir comme l'équation d'amplitude générique d'une déstabilisation de l'équilibre à laquelle nous avons rajouté un terme d'ordre cinq pour représenter la saturation non-linéaire de l'instabilité. Nous avons alors découvert, simulé et interprété des solutions en forme de pulses.